Bayesian network
An example
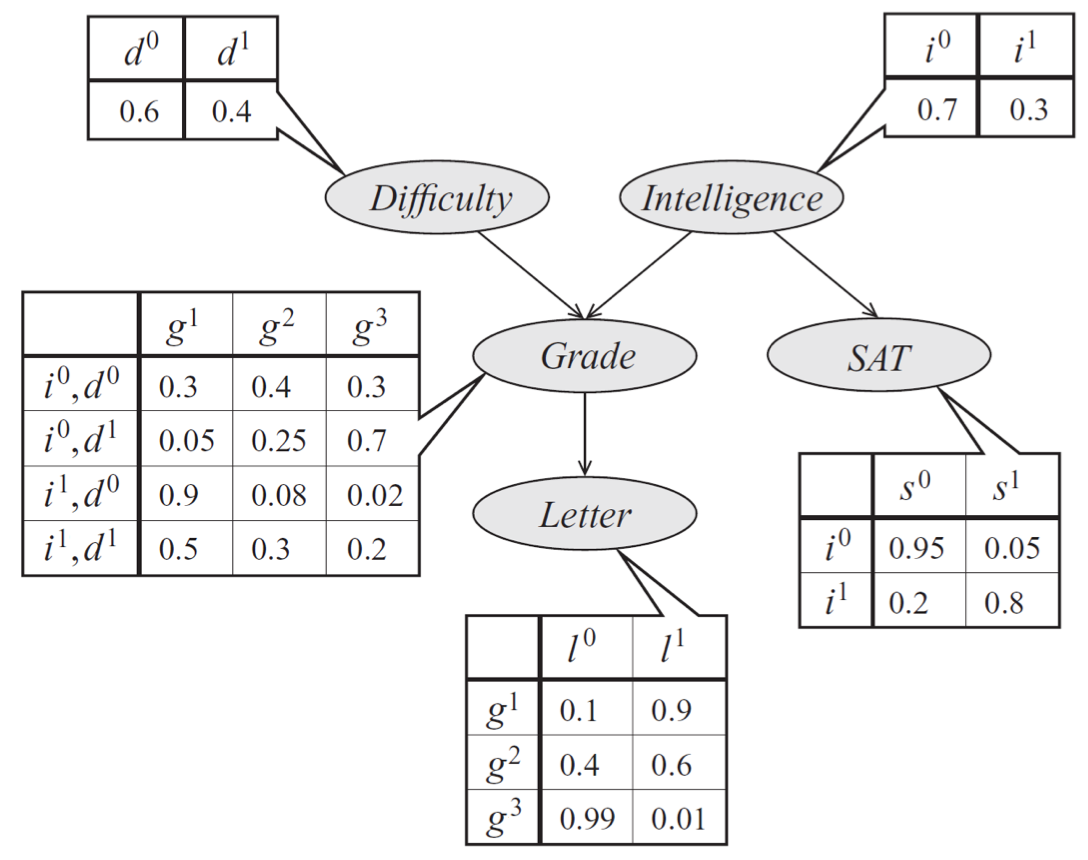
- Causal reasoning
- Evidential reasoning
- Inter-causal reasoning (“explaining away”)
Active trails
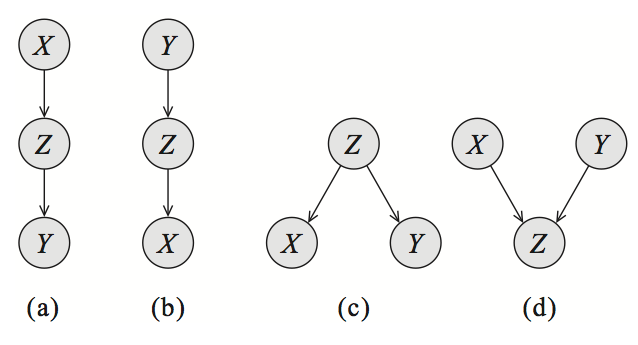
| Active path X-Y | Z unobserved | Z observed |
|---|---|---|
| (a) cascade | ✓ | ✕ |
| (b) cascade | ✓ | ✕ |
| (c) common parent | ✓ | ✕ |
| (d) v-structure | ✕ | ✓ |
A trail $X_1, \dots, X_k$ is active given $Z$ if:
- for any v-struction $X_{i-1} \rightarrow X_i \leftarrow X_{i+1}$, that $X_i$ or one of its descendents $\in Z$
- no other $X_j \in Z$ not at that middle position of a v-structure
Independence and Factorization
A joint probability distribution P factor over a directed acylic graph G if it can be decomposed into a product of factors, as specified by G.
Factorization of a distribution P implies independies that hold in P.
X, Y independent
\[P(X,Y) = p(X)P(Y)\]$(X \perp Y \vert Z)$
\[P(X,Y,Z) \propto \phi_1(X,Z) \phi_2(Y,Z)\]d-separation $\text{d-sep}_{G}{(X,Y\vert Z)}$
X and Y are d-separated in G given Z if there is no active trail in G between X and Y given Z.
If P factorizes over G, and $\text{d-sep}_{G}{(X,Y\vert Z)}$, then P satisfies $(X \perp Y \vert Z)$
General property: Any node is d-separated from its non-descendatns given its parents.
If P factors over G, then in P any variable is independent of its non-descendants given its parents.
I-maps
If P satistifies I(G), we say that G is an I-map of P. \(I(G) = \{(X \perp Y \mid Z) : \text{d-sep}_{G}{(X,Y\vert Z)}\}\)
If P factorizes over G, then G is an I-map for P. If G is an I-map for P, then P factorizes over G.
Dynamic Bayesian Network
Dynamic Bayesian Networks (DBN) are compact representation for encoding structured distributions over arbitrarily long temporal trajectories.
Markov assumption
\[P(x_{0:T}) = P(X_0) \prod_{t=0}^{T-1} P(X_{t+1} \vert X_{0:t})\]Assuming $ (X_{t+1} \perp X_{0:t-1} \vert X_t) $, it becomes
\[P(x_{0:T}) = P(X_0) \prod_{t=0}^{T-1} P(X_{t+1} \vert X_{t})\]Could be extended to semi-markov assumption to model for example velocities of robots.
Time invariance
Template transition model
\[P(X_{t+1} \vert X_{t}) = P(X' \vert X)\]Could be extended with additional variables for abrupt factors like sensor failure, etc.
Dynamic Bayesian Network
A dynamic Bayesian network over $X_1, \dots, X_n$ is defined by:
- For $t = 0$, $ P(X_0) $
- For $t > 0$, $ P(X_t \vert X_{t-1}) = P(X’ \vert X) = \displaystyle \prod_{i=1}^{n} P(X’ \vert \text{Parent}_{X’_i}) $
An example: Online SLAM model has unrolled (ground) model:
- For $t = 0$, $ P(x_0) $
- For $t > 0$, $ P(x_t, z_t \vert x_{t-1}, u_{t}, m) = P(x’, z’ \vert x, u, m) = P(x’ \vert x, u) P(z’ \vert x’, m) $

Hidden Markov Model
To be more specific, the previous online SLAM model is a Hidden Markov Model (HMM). Hidden Markov model in its simplest format can be desribed with the following graph:

where $S_t$ is the hidden random variable at time step $t$ and $O_t$ is the observation at time step $t$.
The transition model represents the probability of the hidden state transiting from one to another $ P(S_t \vert S_{t-1}) = P(S’ \vert S)$.
A simple example of the transition model with four possible states is:

The outgoing edges for each node should sum up to 1, i.e., each row of the transition matrix sum up to 1.
The observation model discribes the probability of observing $O_t$ at time $t$ given the hidden state $S_t$.
Hidden Markov Model could compactly encode temporal sequences by making the assumption that the sequences are generated by a Markov process. For this reason, it is widely used in robot localization, speech recognition, text annotation, etc.
Plate Model
The plate model define a template for an infinite set of Bayesian networks. This helps generalize the same model to similari but different scenarios. For example, two universities might have varying number of students and varying number of courses. But they could share the same plate model to encode student’s grade, intelligence, course difficulty, etc.

For a template variable $A(U_1,\dots,U_k)$ with parents $B_1(U_1),\dots,B_m(U_m)$:
Plate dependency model
For each parent node i, we mush have $U_i \in {U_1, \dots, U_k}$.
For example $G(s, c)$ cannot depend on $I(s, c, u)$.
Ground model
A template CPD $P(A \vert B_1, \dots, B_m) $ is shared by any instantiation of the model, $u_1, \dots, u_k$.
For example $P(G \vert I, D)$ can be applied on any instantiation of the student intelligence and course difficulty.